排列的历史可以上溯到殷周之际的占卜术,较完整的文字记载则见于《易经》.“易”含变化的意思,书中称:“易有太极,是生两仪,两仪生四象,四象生八卦.”“两仪”可用两种基本符号阳爻“—”和阴爻“‐‐”表示,每次取两个,就有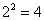 种不同的排列,称为“四象”,即太阳、少阴、少阳、太阴;每次取三个,共有
种不同的排列,称为“四象”,即太阳、少阴、少阳、太阴;每次取三个,共有 种不同的排列,称为“八卦”,即乾≡、兑
种不同的排列,称为“八卦”,即乾≡、兑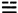 、离
、离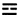 、震
、震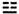 、巽
、巽 、坎
、坎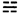 、艮
、艮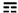 、坤
、坤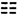 ;若每次取六爻,则可得
;若每次取六爻,则可得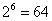 种不同的排列,叫做“六十四卦”.这是一种特殊的排列问题,即从几种事物中每次取
种不同的排列,叫做“六十四卦”.这是一种特殊的排列问题,即从几种事物中每次取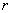 件而允许重复的排列数,答案应是
件而允许重复的排列数,答案应是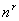 .但是古代没有指数概念,对于很大的
.但是古代没有指数概念,对于很大的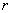 来说,求出答数并非易事.宋代沈括(l031–l095)曾计算过棋局总数,他在《梦溪笔谈》﹝1088年左右﹞中讨论了围棋所有摆出的棋局的总数.唐朝一行﹝683-727﹞计算过这个问题.沈括说:「予尝思之,此固易耳,但数多,非世间名数可能言之」.意思是:「这个问题是很容易解决的,但计算结果,数值太大,是现有的数名无法表达的」.沈括得棋局数为「以一为基,三百六十一次三乘之」.即
来说,求出答数并非易事.宋代沈括(l031–l095)曾计算过棋局总数,他在《梦溪笔谈》﹝1088年左右﹞中讨论了围棋所有摆出的棋局的总数.唐朝一行﹝683-727﹞计算过这个问题.沈括说:「予尝思之,此固易耳,但数多,非世间名数可能言之」.意思是:「这个问题是很容易解决的,但计算结果,数值太大,是现有的数名无法表达的」.沈括得棋局数为「以一为基,三百六十一次三乘之」.即 .这是因为棋盘上每格有三种可能,布黑子、布白子、空格.因此实际的布局数就是三个元素取三百六十一个元素的可重复排列数.无论从这个公式的推导及如此大的数的处理上,沈括的工作都是难能可贵的.
.这是因为棋盘上每格有三种可能,布黑子、布白子、空格.因此实际的布局数就是三个元素取三百六十一个元素的可重复排列数.无论从这个公式的推导及如此大的数的处理上,沈括的工作都是难能可贵的.



印度、阿拉伯在古代也有许多对物体排列组合研究的事例,并且有较深入的认识.公元前300年左右,印度耆那教的文献已提到排列组合问题,他们已经知道了3个排列数和3个组合数(Pn1, Pn2, Pn3 和Cn1, Cn2, Cn3).印度教中的哈利神(Hari)4只手中拿着狼牙棒、铁饼、莲和贝壳,4样的排列不同,哈利神就有不同的名字,共有4!种.
印度数学家巴什迦罗的《立刺瓦提》一书中有一个著名的排列问题:湿婆神(Siva)的十只手中拿十件东西,绳、钩、蛇、鼓、头盖骨、三叉戟、床架、匕首、弓、箭,若十只手交换拿这十样东西,共有多少种不同方式?答案是有3 628 800种,即10!.他首次给出了这一定理,r个物体中,分别有k、l、…个物体相同,则r个物体的排列数为 .
.

用很少几件东西作成的排列方式的数目可能非常大,排列与组合方面的许多问题都是颇有趣的,细心观察你的周围有哪些排列问题.
排列的一个重要特征是“有序性”,即不但要取出元素,而且要按顺序排成一列,顺序不同,是不同的排列.两个排列相同,当且仅当两个排列的元素相同,且元素的排列顺序也相同.
关于排列的问题,基本有两种类型:一类是没有限制条件的;另一类是有限制条件的,即有特殊的元素,不能随意排列,必须满足一定的条件.解决排列问题方法比较多、灵活性强,基本方法有:(1)直接法,一般要结合分类计数原理、分步计数原理和排列数公式,直接进行排列.(2)间接法:先不考虑条件限制全部排列,再从中减去不符合条件的排列.
求解排列问题时应注意三点:
一是弄清题意.要明确题目中的事件是什么,可以通过怎样的“程序”来完成这件事.
二是要弄清问题的限制条件,注意特殊元素和特殊位置.此外还要善于发现隐含的限制条件.如“从0、1、2、3这四个数字中取出三个组成一个三位整数.这样的数有多少个?”这个问题中隐含的一个条件就是“0不能排在百位”,否则,出现诸如“023”的数与“23”是同一个数.
三要合理地分类和分步,设法将交复杂的问题进行分解.
我们重点看一下附有限制条件的排列,求解的思路如下:
(1)对附有限制条件的排列,思考问题的原则是,优先考虑受限制的元素或受限制的位置.
(2)对下列附有限制条件的排列,要掌握基本的思考方法.
元素在某一位置或元素不在某一位置;
元素相邻—捆绑法,即把相邻元素看成一个元素;
元素不相邻—插空法;
比某一数大或比某一数小的问题主要考虑首位或前几位.
(3)对附有限制条件的排列要掌握正向思考问题的方法—直接法;同时要掌握一些问题的逆向思考问题的方向—间接法.
例如:7名同学排队照相.
(1)若分成两排照,前排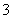 人,后排
人,后排 人,有多少种不同的排法?
人,有多少种不同的排法?
(2)若排成两排照,前排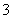 人,后排
人,后排 人,但其中甲必须在前排,乙必须在后排,有多少种不同的排法?
人,但其中甲必须在前排,乙必须在后排,有多少种不同的排法?
(3)若排成一排照,甲、乙、丙三人必须相邻,有多少种不同的排法?
(4)若排成一排照,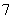 人中有
人中有 名男生,
名男生,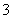 名女生,女生不能相邻,有多少种不面的排法?
名女生,女生不能相邻,有多少种不面的排法?
分析:(1)可分两步完成:第一步,从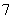 人中选出
人中选出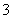 人排在前排,有
人排在前排,有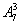 种排法;第二步,剩下的
种排法;第二步,剩下的 人排在后排,有
人排在后排,有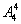 种排法,故一共有
种排法,故一共有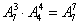 种排法.事实上排两排与排成一排一样,只不过把第
种排法.事实上排两排与排成一排一样,只不过把第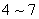 个位子看成第二排而已,排法总数都是
个位子看成第二排而已,排法总数都是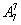 ,相当于
,相当于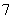 个人的全排列.(2)优先安排甲、乙.(3)用“捆绑法”.(4)用“插空法”.
个人的全排列.(2)优先安排甲、乙.(3)用“捆绑法”.(4)用“插空法”.
解:(1)  种.
种.
(2)第一步安排甲,有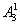 种排法;第二步安排乙,有
种排法;第二步安排乙,有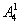 种排法;第三步余下的
种排法;第三步余下的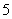 人排在剩下的
人排在剩下的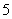 个位置上,有
个位置上,有 种排法,由分步计数原理得,符合要求的排法共有
种排法,由分步计数原理得,符合要求的排法共有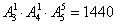 种.
种.
(3)第一步,将甲、乙、丙视为一个元素,有其余 个元素排成一排,即看成
个元素排成一排,即看成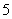 个元素的全排列问题,有
个元素的全排列问题,有 种排法;第二步,甲、乙、丙三人内部全排列,有
种排法;第二步,甲、乙、丙三人内部全排列,有 种排法.由分步计数原理得,共有
种排法.由分步计数原理得,共有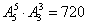 种排法.
种排法.
(4)第一步, 名男生全排列,有
名男生全排列,有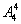 种排法;第二步,女生插空,即将
种排法;第二步,女生插空,即将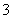 名女生插入
名女生插入 名男生之间的
名男生之间的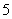 个空位,这样可保证女生不相邻,易知有
个空位,这样可保证女生不相邻,易知有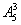 种插入方法.由分步计数原理得,符合条件的排法共有:
种插入方法.由分步计数原理得,符合条件的排法共有: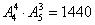 种.
种.
说明:(1)相邻问题用“捆绑法”,即把若干个相邻的特殊元素“捆绑”为一个“大元素”,与其他普通元素全排列;最后再“松绑”,将这些特殊元素进行全排列.(2)不相邻问题用“插空法”,即先安排好没有限制条件的元素,然后再将有限制条件的元素按要求插入排好的元素之间.