二项式定理和杨辉三角有着非常紧密的联系．我们来看下面的算式：

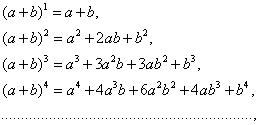
这里，展开后的系数1，3，3，1就是杨辉三角第四行的数字．不难算出的系数是1，6，15，20，15，6，1，即杨辉三角第七行的数字．所以杨辉三角可以看做是二项式的乘方经过分离系数法后列出的表．实际上，我们可以证明这样的事实：一般地说，的展开式的系数就是杨辉三角中第n+1行的数字

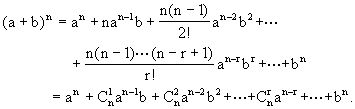
这其实就是有名的二项式定理．对于牛顿非凡的发现，我们在此只能略窥一斑．虽然按照欧几里得或阿基米德的概念来说，这不是一条“定理”，因为牛顿没有提供完整的证明．但是，他的见识和直觉足以使他发明出这一恰当而准确的公式．早在牛顿出生之前很久，人们便已提出并解决了二项式的展开式问题．中国数学家杨辉早在13世纪就发现了二项式的秘密，但他的著作直到近代才为欧洲人所知．这样的三角图形，曾出现在我国宋朝数学家杨辉于1261年著的《详解九章算法》一书中，因此人们就称它为“杨辉三角”．实际上，杨辉三角并不是杨辉发现的，据估计，它的发现不迟于公元1200年．在欧洲，这一图形一般都认为是1654年由帕斯卡发现的，因此称为“帕斯卡三角”．事实上，1527年国外出版的一本数学书上已经出现了这一图形．但无论怎样，杨辉三角的发现，在我国比欧洲至少要早300年左右．维埃特在其《分析术引论》前言的命题XI中也同样论证了二项式问题．但这一伟大发现通常是以布莱兹·帕斯卡的名字命名的．帕斯卡注意到，二项式的系数可以很容易地从我们现在称为“帕斯卡三角”的排列中得到：

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

1 7 21 35 35 21 7 1

…………………………………

在这个三角形中，每一个新增数字都等于其上左右两个数字之和．因此，根据帕斯卡三角，下一行的数值为：1 8 28 56 70 56 28 8 1．

例如，表值56就等于其上左右两个数字21＋35之和．斯卡三角与展开式之间的联系是非常直接的，因为三角形的最后一行数值为我们提供了必要的系数．所以，帕斯卡三角的实用性是非常明显的．

年轻的牛顿经过对二项展开式的研究，发明了一个能够直接导出二项式系数的公式，而不必再繁琐地延伸三角形到所需要的那行了．

对于帕斯卡三角，其实也就是杨辉三角的构成，我们来看如下的例子：

如下图，在一块倾斜的木板上，钉上一些正六角形小木块，在它们中间留下一些通道，从上部的漏斗直通到下部的长方框子．把小弹子倒在漏斗里，它首先会通过中间的一个通道落到第二层六角板上面，以后，落到第二层中间一个六角板的左边或右边的两个竖直通道里去．……

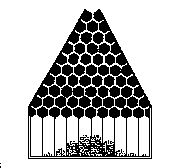
于是，弹子通过每一层每个通道的可能情形是：

第一层1

第二层1 1

第三层1 2 1

第四层1 3 3 1

第五层1 4 6 4 1

………

你能够根据杨辉三角的规律，写出第6层到第10层弹子通过每一通道的可能情形．

现在请你算一算：弹子通过10层通道，落到每个长方形框里的可能情况．

对这类计算“可能性”的问题，与我们过去所学的数学知识，无论在思路上，或是解题方法上都有所不同，它是用“概率”的大小来说明的．概率是用以刻划某一事件发生的可能性大小的数量指标．对必然会发生的事件，它的概率为1；对不可能发生的事件，它的概率为0．例如袋中有一颗红色珠和一颗黄色珠，一次摸出一红一黄两颗珠的可能性，也就是它的概率为1(必然会发生)；一次摸出两颗红色珠的概率为0(不可能发生)；一次摸出一颗红色珠的概率为0.5(一半的可能性)．

其实，中国古代数学家在数学的许多重要领域中处于遥遥领先的地位．中国古代数学史曾经有自己光辉灿烂的篇章，而杨辉三角的发现就是十分精彩的一页．

杨辉，字谦光，北宋时期杭州人．在他1261年所著的《详解九章算法》一书中，辑录了如上所示的三角形数表，称之为“开方作法本源”图，并说它“出释锁算书，贾宪用此术”．贾宪是11世纪人．这就表明，杨辉三角的发现远早于1261年，也不是杨辉首先发现的，而是杨辉之前约200年的贾宪创造的．

科学史上的任何发明创造都有其客观背景和演变过程．杨辉三角的发现渊源于高次方程的数值解法．中国古代数学家们对高次方程数值解法的探索经历了长时期的发展过程．那时候把求解一般方程的数值解法叫作“开方法”．这是因为一般方程的数值解法，都是由开方的方法推演出来的．特别地，开平方和开立方，实际上正是求解和的一种数值解法．早在魏末刘徽作注的《九章算术》中，就有完整的开平方法和开立方法．刘徽探索了这种方法的来源，作出了这种方法的几何解释．例如要求完全平方数55225的平方根，相当于求一面积为55225的正方形的边长．注意到55225的平方根为一个三位数，可设正方形的边长为100a+10b+c（即a、b、c分别为所求平方根的百位、十位、个位上的数字），然后逐一确定a、b、c．为此，刘徽把正方形划分成如图所示的七个部分，其中 1、4、7三部分分别是边长为 100a、10b、c的正方形．

在这以后的数百年中，我国古代数学家们一直没有停止对更高次的开方法的研究．宋元时期是我国古代数学史上群星灿烂的黄金时代，这一时期诞生了许多杰出的数学家，留下了不少出色的数学著作．贾宪就是这一时期的人，他是北宋天文学家楚衍的儿子．贾宪创造了新的开平方法和开立方法，《详解九章算法》称之为“增乘开方法”．

这种方法正是我们今天教科书中介绍的方法．而类似的方法在欧洲则要到1804年和1819年才分别由意大利数学家鲁菲尼与英国数学家霍纳提出，比贾宪迟了大约800年．

贾宪创造的开平方法和立方法摆脱了《九章算术》中刘徽阐释的几何方法的约束，开辟了寻求纯代数法的道路，使得这种“增乘开方法”有可能推广到更高次的情形去．虽然几何直觉启示人们发现了不少新命题和新方法，但是这种直观性的思维对更高维的问题却往往无能为力．《九章算术》中记载的开平方法和开立方法，依靠几何直观，无法解决更高次的开方问题，只有另辟蹊径，才有希望在这里取得突破．在这一领域中，我们的先辈进行了长时期的摸索和试探．从刘徽到贾宪，中间相隔了800年左右的时间．取得这种突破的艰巨性就可想而知了．更加令人自豪的是，《九章算术》提出了完整的开平方法和开立方法后，好像是等待了世界800年，最后还是由中国人自己把这个问题彻底解决．贾宪在找到了开平方和开立方的新方法后，继续向前迈进，终于解决了任意高次幂的开方问题．

用开平方和开立方的“增乘开方法”解决了四次以上的开方问题，首先必须知道四次以上二项展开式的系数．到这时，杨辉三角的诞生就成为非常必要的了．而早已熟知的二次、三次情形下的二项展开式的系数，则又为贾宪探求二项系数所排成的三角形数表的规律准备了富有启发性的特例，从而为贾宪最终完成这一杰作提供了可能条件．从刘徽解释开平方和开立方的几何意义，到贾宪发现杨辉三角，从而完成更高次的开方问题，这实在是合乎逻辑的必然结果．有了杨辉三角，就可以求得任意高次二项展开式的系数，因而也就从理论上来说解决了任意高次的开方问题．早在11世纪中叶便解决了开任意高次幂的开方法问题，这不能不说是中国古代数学家的一项杰出的创造．杨辉的《详解九章算法》收录了许多早已失传的各种数学著作中的一些问题和算法，“增乘开方法”和“开方作法本源”图就是通过杨辉著作的阐释才得于留传至今．在这个意义上，把“开方作法本源”图冠于杨辉之名也是当之无愧的．

总而言之，二项展开式系数所组成的三角形数表的发现，即使似文字记载为依据，也是1261年杨辉的《详解九章算法》为最早的记录．在中亚细亚，阿尔·卡西载有类似数表的《算术之钥》发表于1427年，而欧洲首先发现的这种数表，是印在1527年德国数学家阿皮纳斯所著的一本书的封面上．《详解九章算法》比它们早了二三百年．如果从11世纪的贾宪算起，则早于它们四五百年．