|
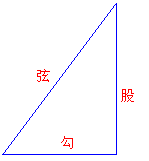
勾股定理又称“商高定理”,是指“在直角三角形中,两条直角边的平方和等于斜边的平方”.其逆定理是“在三角形中,如果两边的平方和等于第三边的平方,那么这个三角形是直角三角形”.勾股定理是初等几何中的一个基本定理,有十分悠久的历史,几乎所有文明古国(希腊、中国、埃及、巴比伦、印度等)对此定理都有所研究.
在我国西汉或更早时期的天文历算著作《周髀算经》中,第一章记述了西周开国时期(约公元前1000年)商高和周公姬旦的问答.周公问商高:“天不可阶而升,地不可将尽寸而度.”天的高度和地面的一些测量的数字是怎么样得到的呢?商高回答:“故折矩以为勾广三,股修四,径隅五.”即我们常说的勾三、股四、弦五.《周髀算经》里还这样记载:周髀长八尺,夏至之日晷一尺六寸.髀者,股也,正晷者,勾也.正南千里,勾一尺五寸,正北千里,勾一尺七寸.日益表南,晷日益长.候勾六尺,即取竹,空经一寸,长八尺,捕影而观之,室正掩日,而日应空之孔.由此观之,率八十寸而得径寸,故此勾为首,以髀为股,从髀至日下六万里而髀无影,从此以上至日,则八万里.这段文字描述了中国古代人民如何利用勾股定理在科学上进行实践.
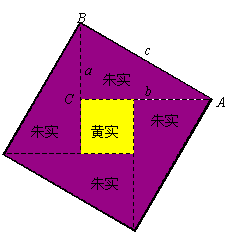
“勾股定理”在西方被称为“毕达哥拉斯定理”,相传是古希腊数学家兼哲学家毕达哥拉斯(Pythagoras,公元前572?~公元前497?)于公元前550年首先发现的.毕达哥拉斯有次应邀参加一位富有政要的餐会,这位主人豪华宫殿般的餐厅铺着是正方形美丽的大理石地砖,由于大餐迟迟不上桌,这些饥肠辘辘的贵宾颇有怨言;但这位善于观察和理解的数学家却凝视脚下这些排列规则、美丽的方形磁砖,但毕达哥拉斯不只是欣赏磁砖的美丽,而是想到它们和数之间的关系,于是拿了画笔并且蹲在地板上,选了一块磁砖以它的对角线 AB为边画一个正方形,他发现这个正方形面积恰好等于两块磁砖的面积和.他很好奇,于是再以两块磁砖拼成的矩形之对角线作另一个正方形,他发现这个正方形之面积等于5块磁砖的面积,也就是以两股为边作正方形面积之和.至此毕达哥拉斯作了大胆的假设:任何直角三角形,其斜边的平方恰好等于另两边平方之和.那一顿饭,这位古希腊数学大师,视线都一直没有离开地面.就这样毕达哥拉斯定理也发现了勾股定理. 他发现勾股定理后高兴异常,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此勾股定理又叫做“百牛定理”.勾股定理流传最广的证明载于欧几里得(Euclid,是公元前三百年左右的人)的《几何原本》中,欧几里德在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为“毕达哥拉斯定理”,以后就流传开了. 人类对勾股定理的认识,少说也超过 4000 年!现在共有超过300 种方法证明这定理! 中国古代的数学家们不仅很早就发现并应用勾股定理,而且很早就尝试对勾股定理作理论的证明.最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽.赵爽创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明(右图).赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四.以勾股之差自乘为中黄实.加差实,亦成弦实.在这幅“勾股圆方图”中,以弦为边长得到正方形是由4个相等的直角三角形再加上中间的那个小正方形组成的.每个直角三角形的面积为
赵爽的这个证明可谓别具匠心,极富创新意识.他用几何图形的截、割、拼、补来证明代数式之间的恒等关系,既具严密性,又具直观性,为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范. 我们再看一种典型的证明:
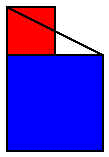
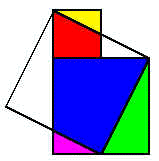
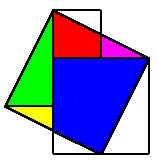
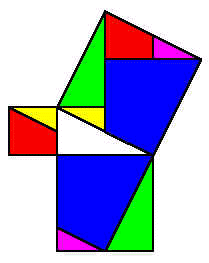
如上图 (a),我们先画一个直角三角形,然后在最短的直角边旁向三角形那一边加上一个正方形,为了清楚起见,以红色表示.又在另一条直角边下面加上另一个正方形,以蓝色表示.接着,以斜边的长度画一个正方形,如上图 (b).我们打算证明红色和蓝色两个正方形面积之和,刚好等于以斜边画出来的正方形面积. 留意在上图(b)中,当加入斜边的正方形后,红色和蓝色有部分的地方超出了斜边正方形的范围.现在我将超出范围的部分分别以黄色、紫色和绿色表示出来.同时,在斜边正方形内,却有一些部分未曾填上颜色.现在依照上图(c)的方法,将超出范围的三角形,移入未有填色的地方.我们发现,超出范围的部分刚好填满未曾填色的地方!由此我们发现,上图(a)中,红色和蓝色两部分面积之和,必定等于上图(c)中斜边正方形的面积.由此,我们就证实了勾股定理. 这个证明是由三国时代魏国的数学家刘徽所提出的.在魏景元四年(即公元 263 年),刘徽为古籍《九章算术》作注释.在注释中,他画了一幅像上图(b)中的图形来证明勾股定理.由于他在图中以「青出」、「朱出」表示黄、紫、绿三个部分,又以「青入」、「朱入」解释如何将斜边正方形的空白部分填满,所以后世数学家都称这图为「青朱入出图」.亦有人用「出入相补」这一词来表示这个证明的原理. 在历史上,以“出入相补”的原理证明勾股定理的,不止刘徽一人,例如在印度、在阿拉伯世界、甚至乎在欧洲,都有出现过类似的证明,祇不过他们所绘的图,在外表上,或许会和刘徽的图有些少分别.下图中,就是将上图(b)和上图(c)两图结合出来的.
但毕达哥拉斯对勾股定理的证明方法已经失传.著名的希腊数学家欧几里得(Euclid,公元前330~公元前275)在巨著《几何原本》(第Ⅰ卷,命题47)中给出一个很好的证明.
在图一中, 这个证明巧妙地运用了全等三角形和三角形面积与长方形面积的关系来进行.不单如此,它更具体地解释了,“两条直角边边长平方之和”的几何意义,这就是以 ML 将正方形分成 BMLD 和 MCEL 的两个部分! 请你自己在查找一些勾股定理证明的方法. |



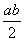 ;中间的小正方形边长为
;中间的小正方形边长为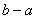 ,则面积为
,则面积为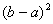 .于是便可得如下的式子:
.于是便可得如下的式子: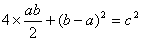 ,化简后便得
,化简后便得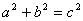 .
.


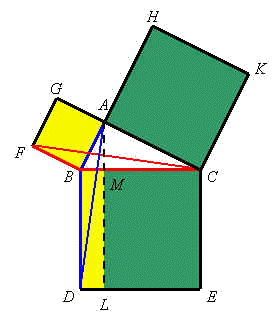
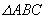 为一直角三角形,其中
为一直角三角形,其中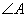 为直角.我们在边AB、BC 和 AC 之上分别画上三个正方形 ABFG、BCED 和 ACKH.过 A 点画一直线AL使其垂直于DE并交 DE 于L,交BC于M.不难证明,
为直角.我们在边AB、BC 和 AC 之上分别画上三个正方形 ABFG、BCED 和 ACKH.过 A 点画一直线AL使其垂直于DE并交 DE 于L,交BC于M.不难证明,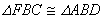 (S.A.S.).所以
(S.A.S.).所以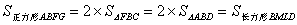 .类似地,
.类似地,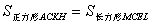 .即
.即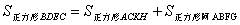 ,亦即是
,亦即是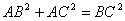 .由此证实了勾股定理.
.由此证实了勾股定理.