|
转化的思想在数学中应用十分广泛,例如,我们将二元方程组通过消元变为一元方程,将二次方程降次为一次方程等,解题的本质就是转化,我们在解数学题时,碰到陌生的问题常把它设法转化成熟悉的问题,碰到复杂的问题常设法把它转化成简单问题,从而使问题获得解决。若想完成这种转化,就应联想到相关的另一事物。联想起与之类似的问题,类似的形式,类似的解法,或者联想类似的定理,公式或法则,并将待解决的问题与联想起来的问题进行比较,类比,推理……达到转化的目的。在解直角三角形这一部分,许多题目也要通过转化达到解题目的。
例1.如图,在ΔABC中, ∠C=90°,∠A的平分线交BC于D,则  等于( ) 等于( )
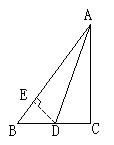
A、sinA B、cosA C、tanA D、cotA
分析:要判断  的比是∠A的哪一个三角函数,联想锐角三角函数定义,首先考虑 的比是∠A的哪一个三角函数,联想锐角三角函数定义,首先考虑  等于哪两条线段的比?再联想角平分线的性质,在图中作出表示AB-AC的线段,为此,作DE⊥AB于E,由∠C=90°,可得RtΔADE≌RtΔADC,所以AC=AE,DE=DC,于是BE=AB-AC,又∠BDE =90°-∠B=∠A, 等于哪两条线段的比?再联想角平分线的性质,在图中作出表示AB-AC的线段,为此,作DE⊥AB于E,由∠C=90°,可得RtΔADE≌RtΔADC,所以AC=AE,DE=DC,于是BE=AB-AC,又∠BDE =90°-∠B=∠A,
∴  = = 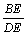 =tan∠BDE=tanA,或由 =tan∠BDE=tanA,或由 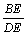 =cotB=tanA。故选C。 =cotB=tanA。故选C。
例2.如图所示,在ΔABC中,∠B=60°,且∠B所对的边b=1,AB+BC=2,求AB的值。
分析:欲求AB的值,题目是斜三角形,已知条件非常分散,所以若想用到角的条件,必须构造直角三角形,作BC上的高AD,把问题转化成解直角三角形。

解:作AD⊥BC于D,设BD=x,在RtΔABD和RtΔACD中,
∵∠B=60°, ∴AB=2x, AD= 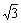 x, DC= x, DC=  = =  , ,
∴ AB+BC=2x+x+  =3x+ =3x+  =2 =2
解得:x= 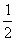 , ,
经检验是原方程的根,
则AB=2x=1
此题目实际上还用到了方程的思想。
例3.已知:如图,在ΔABC中,∠B=60°,∠C=45°,BC=5,求ΔABC的面积。
分析:欲求ΔABC的面积,问题转化为求出BC边上的高AD。这就转化为解直角三角形。由AD=DC,tanB= 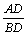 ,于是可构造一个方程去解。 ,于是可构造一个方程去解。
解:作AD⊥BC于D,∠C=45°,
∴ AD=DC,设AD=x,
则DC=x, BD=5-x,
又∠B=60°,
∴ tanB= 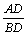 = =  , ,
∴  = = 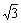 . .
解之,得 x= 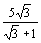 = = 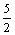 (3- (3- 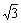 ). ).
∴SΔABC= 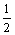 BC·AD= BC·AD=  (3- (3- 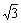 ) )
评述:以上两题通过添加辅助线,把斜三角形的转化为直角三角形,同时巧设未知数构造方程使问题获得解决。
例4.如图,ΔABC中,∠A=90°,AB=AC,D是AC上的一点,且AD∶DC=1∶3,求tan∠DBC的值。
分析:此题的特征,在条件中没有给出有关线段的长度,又tan∠DBC的值不能从给定直角三角形中得到,因此,给解题带来了困难,但我们可以通过构造一个直角三角形及构造方程可求得tan∠DBC的值。

解:作DE⊥BC于D,并设AD=k,DC=3k,AB=AC=4k,
∵∠A=90°,∴BC=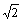 AC=4 AC=4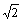 k,又∠C=45° k,又∠C=45°
∴∠EDC=45°, DE=EC,
在RtΔDEC中,DE2+EC2=DC2,
设DE=x,则x2+x2=9k2,
x2= k2, x= k2, x=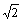 k(负值舍去) k(负值舍去)
∴ DE=EC=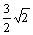 k, k,
∴ BE=BC-EC=4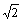 k- k-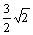 k= k=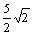 k, k,
∴tan∠DBE=  = = 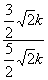 = = 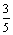 。 。
说明:将已知条件中的比值1:3设为1k、3k,是常用的方法,这样可使得两线段的比转化为两线段,应用方便。
|




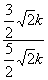 =
=