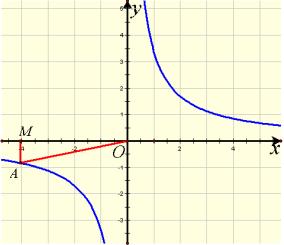
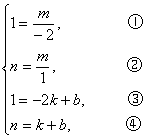| 反比例函数是刻画两个变量之间的数量关系和变化规律的一种常用的数学模型.如,在锻造体积为16的长方体过程中,底面一边长固定为2,则另一边长y与高x间的函数关系 你知道反比例系数k的几何意义吗? 例 一个反比例函数在第三象限的图象如图所示,若A是图象上任意一点,
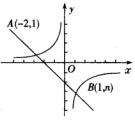
分析:由 解:因为 又因为双曲线在第一、三象限,则 所以,反比例函数的关系式为 说明:由于反比例函数的系数可能为正,也可能为负,所以求解时一定要加上绝对值. 反比例函数的图象有什么特点?有哪些性质? 利用下面提供的动画探究反比例函数的图象和性质. 下面通过例题进一步理解反比例函数的图象特点与性质. 例1 已知反比例函数 (1)若该函数图象经过点(2,-1),求k的值. (2)若该函数图象在每一象限内y随x的增大而减小,求k的取值范围. 分析与解:(1)因为函数经过点(2,-1),把点(2,-1)代入解析式,得 (2)由题意,该函数图象在每一象限内y随x的增大而减小,可知,函数的图象应分布在一、三角限中,所以 所以k的取值范围是 例2 如图所示,一次函数
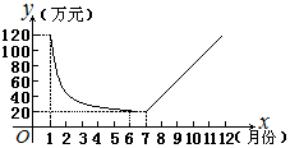
(1)利用图中条件,求反比例函数和一次函数的解析式; (2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围. 分析:由图象知,一次函数和反比例函数的图象都经过 解:(1)解法1 把 ∴ ∴反比例函数解析式为 把 将A、B坐标代入 ∴一次函数解析式为 解法2 因为A、B两点都在双曲线 ∴ 解这个方程组,由①,得 将 由③、⑤组成方程组 解这个方程组,得 ∴反比例函数解析式为 (2)由图象和(1)知,反比例函数和一次函数图象的交点坐标为(-2,1),(1,-2),即 反比例函数的应用 反比例函数是描述变量之间相互关系的重要数学模型之一.很多实际问题可以归结为反比例函数问题来解决. 当变量之间存在反比例关系时,用反比例函数的知识去处理,能较好地运用函数的性质和思想方法.因此,在很多反比例问题中,常要综合运用反比例函数知识来解决问题. 用反比例函数解决实际问题,首先要分析问题情景,建立有关的数学模型,有时还要与其他的有关知识综合起来运用,使问题得到圆满解决. 例1 如图所示,某公司2003年1月份的产值达120万元.由于经营不善,公司出现亏损,每月的利润y(万元)与时间x(月份)成反比例关系下降.至6月底,降至20万元.公司及时采取措施,制止了利润下滑趋势,使7月份的利润保持与6月相同,以后公司进行了一系列的改革措施,从7月底后,公司每月的利润呈直线上升,8月份达到36万元.
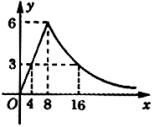
(1)照这样的速度发展,在什么时候公司的月利润全达到100万元? (2)如果公司提前采取措施,在3月底就开始整顿,也就是4月份的利润保持与3月相同,以后每月的利润同样呈直线回升,5月比4月增加16万元.那么到2003年的第几个月,这个公司的利润就会超过100万元? 分析与解:(1)由题意可知:6月底到7月底的利润保持20万元,所以点(7,20)在直线上;又在8月底达36万元,所以点(8,36)也在直线上.由两点可以求出7月后利润的函数关系式. 设直线解析式为 把y=100代入解析式,得x=12. 所以在2003年12月底,公司利润达到100万元. (2)由题不难得到反比例函数解析式为 把x=3代入,得y=40,即3月份的利润为40万元. 同(1),设5月后的利润直线为 但在整顿后的1个月中,公司的利润保持不变,1个月后利润才稳步上升.所以点(4,40)在直线上,而不是点(3,40).又,易知,点(5,56)也在直线上.从而可知直线的函数关系式为y=16x-24. 根据题意,令16x-24>100,解得 所以从03年8月起,公司月利润将超过100万. 思考:利用图象反映的实际问题中数量之间的关系,解决一些实际问题,你体会到知识来源于实践,应用于实践的过程了吗? 说明:实际问题中的两个变量之间的关系我们常转化为有关函数的问题,函数是描写实际问题的一种典型的数学模型和常用工具. 例2 为了预防“非典”,某学校对教室采用药熏进行消毒.已知药物燃烧时,室内每立方米的含药量y(毫克)与时间x(分钟)成正比例.药物燃烧后,y与x成反比例(如图所示).
现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中所提供的信息,解答下列问题: (1)求药物燃烧时,y关于x的函数关系式,自变量x的取值范围,以及药物燃烧后,y关于x的函数关系式. (2)研究表明,当空气中每立方米的含药量低于1.6毫克时,学生方可进教室,那么从消毒开始,至少需要经过多少分钟后,学生才能回到教室. (3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么这次消毒是否有效?为什么? 分析:题设中所给的图象是由一个正比例函数和一个反比例函数的各一段图象构成的.根据图象上的一个点的坐标(8,6),可得出反比例函数和正比例函数的函数关系式. 解:(1)设正比例函数函数关系式 设反比例函数函数关系式为 所以,函数关系式为 (2)当y=1.6时,x=30. 所以,30分后学生才能回到教室. (3)此次消毒有效. 把y=3代入 把y=3代入 因为16-4=12>10,即空气中的含药量不低于 说明:根据函数的图象求函数的某些值,研究函数y随自变量x的变化规律是数形结合思想的具体体现. |